Die Herausforderung der OP_Return-Richtlinie: Bilder in der Blockchain

Abstract

Wir beleuchten erneut das Thema der OP_Return-Richtlinie und die damit verbundene Frage der Bildspeicherung in der Blockchain. Diese Diskussion ist weiterhin aktuell, da bis zu 17 % der Nodes Bitcoin Knots verwenden, ein Client, der das Filtern von Bildern unterstützt. Wir erörtern die „Informationstheorie“ und erklären, wie Bilder in gefälschten Bitcoin-Adressen eingebunden werden können und warum es unpraktisch ist, diese Praxis zu verhindern. Darüber hinaus zeigen wir, dass private Schlüssel ebenfalls als Zufallsdaten fungieren, in denen Bilder gespeichert werden können. Ein Beispiel-Transaktionsvorgang wird erstellt, der ein noch „unaufhaltsameres Bild“ in den privaten Schlüsseln enthält, wobei absichtlich anfällige private Schlüssel verwendet werden, sodass sie anhand der auf der Blockchain verfügbaren Daten berechnet werden können.

Überblick

Im Juni 2025 haben die Entwickler von Bitcoin Core einen Pull-Request genehmigt, der im Wesentlichen die Größenbegrenzung von OP_Return in der Software abgeschafft hat. Wir haben bereits darüber geschrieben und vertreten die Auffassung, dass der Gebührmarkt langfristig das geeignete Mittel ist, um Spam zu bekämpfen, nicht Richtlinienbeschränkungen und Filter. Die Entscheidung, die OP_Return-Größenbegrenzung aufzuheben, ist unter bestimmten Bitcoin-Nutzern umstritten. Einige behaupten, dies fördere Spam-Transaktionen, wie z.B. JPG-Bilder. Kritisiert wird zudem, dass die Entwickler von Core nicht ausreichend gegen Spam vorgehen und nichts unternommen haben, um JPGs auf der Blockchain zu verhindern. Als Udi Wertheimer die Anti-Spam-Gemeinschaft herausforderte, indem er Bilder in Form von „Taproot Wizards“ auf der Blockchain platzierte, hoffte die pro-Filter-Gruppe darauf, dass die Entwickler von Bitcoin Core handeln würden, was jedoch nicht geschah. Infolgedessen nutzen immer mehr Menschen Bitcoin Knots, einen Client, der angeblich mehr gegen Spam unternimmt. Laut Daten von Coin.Dance waren am 25. August 2025 etwa 17 % der erreichbaren Nodes Bitcoin Knots.

Informationstheorie

Während einige die Entwickler von Bitcoin Core dafür kritisierten, dass sie nicht gegen die Bilder vorgehen, entgegneten andere, dass diese nicht „Whack-a-Mole“ spielen sollten, da dies Zeitverschwendung sei. Dies bedeutet, dass die Entwickler von Bitcoin Core zwar etwas gegen die Bilder unternehmen könnten, dies jedoch nur vorübergehend effektiv wäre, da die Spinner immer einen Weg finden würden, sich der Verteidigung zu entziehen. Es ist ein asymmetrischer Kampf, da die Spammer für jeden ihrer Schritte weit weniger Aufwand betreiben müssen als die, die versuchen, den Spam zu stoppen. Es handelt sich um einen Krieg, der schlussendlich zu einem Ende führen wird, in dem die Spammer siegen werden. Warum sollten die Entwickler von Bitcoin Core verpflichtet sein, Zeit und Mühe in einen Kampf zu investieren, den sie letztendlich verlieren würden? Daher ist es verständlich, dass viele Entwickler nicht in diesem Kampf tätig werden wollen. Aus der Perspektive der Pro-Filter erkennen sie dies wahrscheinlich an, argumentieren jedoch, dass die Filter dazu da sind, die Kosten für Spam zu erhöhen, selbst wenn sie umgangen werden können.

Wenn es darum geht, Spam mit Filtern zu stoppen, könnte man argumentieren, dass dies ein verlorener Kampf ist, was auf der „Informationstheorie“ beruht. Diese Theorie wurde in den 1940er Jahren von Claude Shannon formuliert und beschäftigt sich mit der Übertragung von Informationen. Claude Shannon führte einige der Kernkonzepte in der Informatik und der Informationsübertragung ein. Daher könnte es als etwas unangemessen angesehen werden, die Pro-Filter als definitiv falsch zu betrachten, allein aufgrund der „Informationstheorie“. Vielmehr könnte man sagen, dass diese Theorie als Wissenschaftsfeld betrachtet werden kann, in dem man argumentieren könnte, dass Bilder immer in scheinbar zufälligen Daten gespeichert werden können, die für Bitcoin-Transaktionen benötigt werden. Es ist wahrscheinlich nicht gerecht zu sagen, dass die „Informationstheorie“ hier etwas beweist.

Auf der grundlegendsten Ebene haben finanzielle Bitcoin-Transaktionen einige notwendige Komponenten, die sicherstellen, dass die Transaktionen funktionieren. Jede Transaktion benötigt nämlich einen öffentlichen Schlüssel und eine Signatur. Es ist unklar, wie Bitcoin ohne diese beiden Kernkomponenten funktionieren kann. Diese Komponenten müssen mindestens on-chain sein. Beim Empfang von Bitcoin gibt man eine Bitcoin-Adresse an. Da diese Adressen durch eine Hash-Funktion generiert werden, sind sie also nicht von zufälligen Daten zu unterscheiden. Bildbezogene Daten können daher als „falsche Adresse“ verwendet werden, an die Coins gesendet werden können. Diese gefälschten Adressen werden dann in Form eines Output-Hashes in die öffentliche Blockchain eingetragen. Diese Coins können nie zurückgeholt werden, da kein bekannter öffentlicher Schlüssel mit den Adressen verknüpft ist, an die sie gesendet wurden. Das Verständnis dieses Sachverhalts kann als „Informationstheorie“ betrachtet werden, da eine Hash-Funktion ein zufälliger Prozess ist, der Entropie erzeugt, die zur Übertragung von Informationen verwendet werden kann. Dies kann wirklich nicht gestoppt werden, egal welche Filter verwendet werden. Solche gefälschten Adressen wurden bereits in der Vergangenheit in Bitcoin verwendet, einige Beispiele sind nachfolgend aufgeführt.

Gefälschte Adressen

Im Dezember 2013 wurde der Prozess der „falschen Adresse“ genutzt, um ein Bild des ehemaligen südafrikanischen Präsidenten Nelson Mandela in die Bitcoin-Blockchain einzufügen. Dieses Bild sehen Sie unten.

Bereits 2011 wurden gefälschte, nicht ausgebbare Adressen verwendet, um das Bitcoin-Logo in der Bitcoin-Blockchain zu speichern.

Es sollte angemerkt werden, dass Spam wie dieser, mit gefälschten Adressen, es schwieriger macht, einen Node zu betreiben, da es das UTXO-Set aufblähen kann. Dies ist Teil der Begründung für die Zulassung von OP_Return.

Verbot von gefälschten Adressen

Wenn jemand die gefälschten Adressen stoppen möchte, könnte dies tatsächlich möglich sein. Es würde jedoch eine grundlegende Umstrukturierung von Bitcoin und eine Änderung des Bitcoin-Protokolls erfordern. Um solche Adressen zu blockieren, könnte man verlangen, dass die Transaktionsausgaben eine digitale Signatur enthalten, die belegt, dass es ein Paar aus öffentlichem und privatem Schlüssel gibt und dass die Adresse „echt“ ist. Sowohl Transaktionsinputs als auch -outputs würden eine Signatur benötigen.

Während dies theoretisch funktionieren könnte, ist dies eine monumentale Aufgabe und hat folgende Nachteile:

• Alle bestehenden Wallets wären mit dem neuen Transaktionsformat inkompatibel, alte Transaktionen wären verboten. Eine solche Verbannung ist in der Vergangenheit nicht erfolgt; die monetäre Souveränität würde bedroht und Menschen könnten ihre Gelder verlieren.

• Der Transaktionsprozess müsste geändert werden, da der Empfänger dem Sender nicht nur eine Adresse, sondern auch eine digitale Signatur zur Verfügung stellen müsste.

• Es wären mehr Signaturen on-chain erforderlich, was zu größeren Transaktionsgrößen führen würde und die Skalierungseigenschaften von Bitcoin schädigen könnte.

• Die Wiederverwendung von Adressen könnte gefördert werden, was die Privatsphäre gefährden könnte.

• Dies wäre eine Protokolländerung und würde eine weitreichende Zustimmung erfordern. Wahrscheinlich müsste es ein Hardfork sein.

• Viele der Funktionen in Bitcoin, wie P2SH oder Taproot, müssten möglicherweise entfernt werden. Oder zumindest könnten wir nicht von den Vorteilen von P2SH profitieren.

• Bitcoin wäre durch mehr sichtbare öffentliche Schlüssel anfälliger für Quantenangriffe.

Wie man sieht, wäre das oben Beschriebene völlig unpraktikabel und eine absolute Katastrophe. Aber selbst diese extreme Änderung könnte die JPGs nicht stoppen. Nach gründlicher Prüfung aller anderen Optionen könnte man immer noch Bilder in privaten Schlüsseln speichern, denn schlussendlich sind private Schlüssel ebenfalls Zufallsdaten und notwendige Komponenten für Bitcoin. Folglich wäre dies weiterhin ein verlorener Kampf für die Entwickler von Bitcoin. Sie hätten sich auf eine gewaltige Aufgabe eingelassen, um Bitcoin und alle Wallets vollständig neu zu strukturiere, nur damit die Spammer relativ leicht auf etwas anderes umsteigen könnten.

JPGs als private Schlüssel

Ein Bitcoin-Privatschlüssel ist lediglich eine zufällige 256-Bit-Zahl. Eine solche Zahl ist mathematisch äquivalent zu einem 16 x 16 Pixel großen Bild, bei dem jeder Pixel entweder schwarz oder weiß ist. Alle Privatschlüssel können durch diese winzigen Bilder dargestellt werden. Wir haben einen Bitcoin-Privatschlüssel erstellt, indem wir ein solches Bild erstellt haben, das unten gezeigt wird, ein Bild einer Person. Wir haben das Bild im JPG-Format gespeichert.

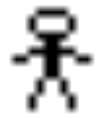
Während das Zeichnen eines Bildes zur Generierung eines privaten Schlüssels nicht immer der sicherste Weg ist, um Bitcoin zu nutzen, könnte dies aus der Pro-Filter-Perspektive als illegitim angesehen werden. Es könnte als Spam gelten, da wir aus bestimmten Blickwinkeln JPGs in die Blockchain einfügen oder JPGs in der Blockchain verwenden. Natürlich ist es jedoch mathematisch unmöglich, die Nutzung von Bitcoin auf diese Weise einzuschränken, da diese Bilder mathematisch äquivalent zu anderen Möglichkeiten sind, private Schlüssel auszudrücken.

Um einen privaten Schlüssel aus dem Bild zu erstellen, kann jedem Pixel eine Eins oder Null zugewiesen werden, je nachdem, ob er schwarz oder weiß ist, wie die folgende 256-Bit-Zahl zeigt.

0000000000000000
0000011111100000
0000100000010000
0000100000010000
0000011111100000
0000000110000000
0000011111100000
0001100110011000
0000000110000000
0000000110000000
0000000110000000
0000001001000000
0000001001000000
0000010000100000
0000010000100000
0000000000000000

Eine der vielen Bitcoin-Adressen, die sich aus dem obigen privaten Schlüssel ergibt, ist wie folgt:

1JfvNAje3G3Gvt41hL4P7Eh96NLj79o5v7

Dies ist nur die Verwendung eines privaten Schlüssels, um ein kleines Bild zu erzeugen. Natürlich könnte man dies auch vergrößern. Man könnte ein großes 1MB-Bild generieren und dieses in Tausende von privaten Schlüsseln aufteilen. Diese könnten in Transaktionen verwendet werden und die Blockchain mit Spam füllen. Dies wird wahrscheinlich als Spam angesehen, während das Erstellen eines einzigen Bildes als privater Schlüssel und die Verwendung zur Verarbeitung von „finanziellen Transaktionen“ von niemandem, selbst von den extremsten Pro-Filter-Anhängern, als Spam angesehen werden kann, auch wenn es mit einem Bild verbunden ist.

Schwache Signaturen

Die oben beschriebene Methode, „Bilder“ on-chain zu setzen, ist nicht besonders effektiv. Zum einen sollen private Schlüssel geheim bleiben, während die Spammer die Bilder öffentlich sichtbar haben möchten. Allerdings kann man eine unsichere Signatur erzeugen, sodass der private Schlüssel aus den on-chain-Daten berechnet werden kann. Wenn die Bilddaten aus den auf der Blockchain verfügbaren Daten ermittelt werden können, ist dies im Grunde genommen das Einfügen von Bildern in die Blockchain.

Um eine Nachricht mit ECDSA zu signieren, müssen verschiedene Berechnungen durchgeführt werden, die Bestandteil des Prozesses zur Generierung einer Signatur sind. Eine der Berechnungen erfordert einen zufällig generierten Wert, K. In der Geschichte von Bitcoin gab es verschiedene Sicherheitsprobleme, bei denen schlechte Zufälligkeit zur Generierung von K verwendet wurde, zum Beispiel ein Problem mit der Blockchain.info-Wallet im August 2013. Aufgrund eines Sicherheitsfehlers wurde derselbe K-Wert verwendet, um mehrere Transaktionen zu signieren. Diese Schwachstelle führte zum Diebstahl von Benutzergeldern. Ein weiteres Beispiel für die Verwendung derselben K-Werte für verschiedene Nachrichten war Sony’s Playstation 3, die denselben K-Wert für jedes Spiel verwendete. Diese Schwachstelle wurde beim Chaos Computer Congress 2010 in Deutschland aufgedeckt. Der legendäre Hacker George Hotz veröffentlichte einige Tage später die privaten Playstation 3-Schlüssel. Daher ist es entscheidend, dass der K-Wert sowohl geheim als auch für jede Nachricht unterschiedlich ist, sonst kann jeder den privaten Schlüssel berechnen.

Wir entwickelten ein einfaches Schema unter Verwendung dieser schwachen K-Werte, um ein JPG-Bild in unseren privaten Schlüsseln zu speichern, sodass diese privaten Schlüssel von jedem berechnet werden können, der Zugang zur Blockchain hat. Anschließend platzierten wir ein JPG-Bild in der Blockchain, indem wir unsere Transaktion sendeten. Wir glauben, dass dies das erste signifikante Bild ist, das in verletzlichen privaten Schlüsseln in der Geschichte von Bitcoin gespeichert wurde. Wir erstellten einen 15 von 15 P2SH-Multisignatur-Input in einer Transaktion mit einem Input und einem Output. Die gesamte Transaktionsgröße beträgt 1690 Bytes. Da der Input ein 15 von 15-Multisignatur-Input ist, gibt es 15 Signaturen und 15 öffentliche Schlüssel in der Blockchain. 14 der 15 verbundenen privaten Schlüssel sind ein JPG-Bild, das das oben dargestellte Bild ist. In Anlehnung an das Bild von 2011 ist es das Bitcoin-Logo in Schwarz-Weiß.

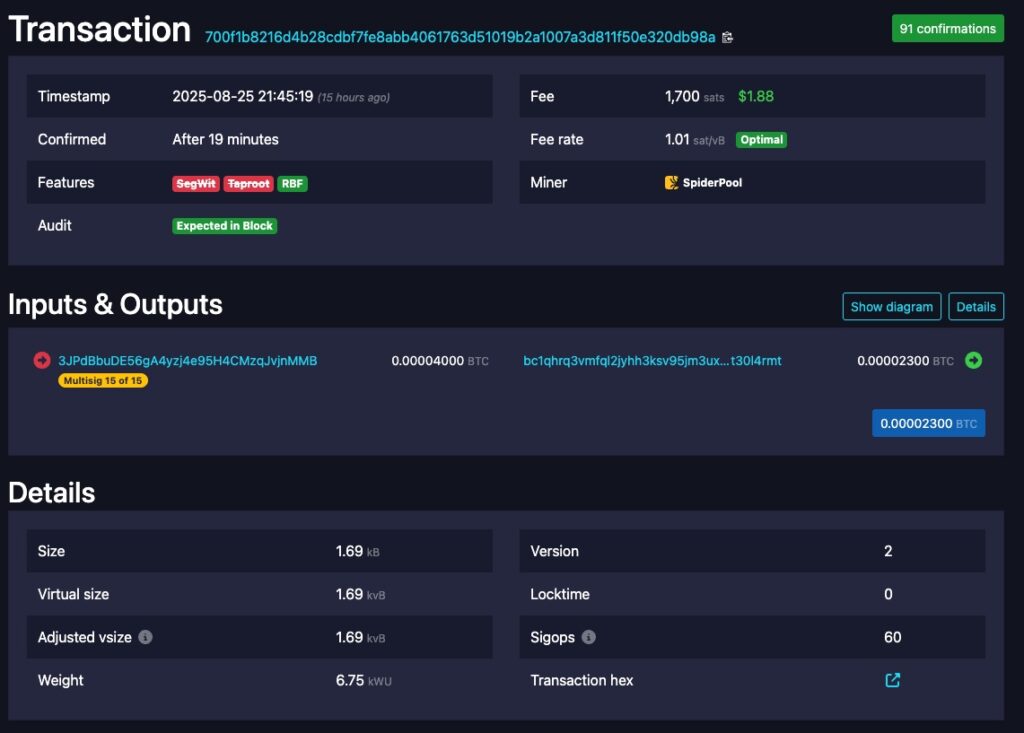
In unserem Ansatz zur Erstellung schwacher Signaturen haben wir nicht denselben K-Wert für mehrere Nachrichten verwendet. Wir wählten ein System, in dem:

• Der erste K-Wert ist ein SHA256-Hash des ersten öffentlichen Schlüssels.

• Der zweite K-Wert ist ein SHA256-Hash des ersten K-Werts.

• Der dritte K-Wert ist ein SHA256-Hash des zweiten K-Werts.

• Und so weiter…

• Der 15. K-Wert ist eine tatsächlich sicher generierte Zufallszahl.

Auf diese Weise sehen die Signaturen für einen Gelegenheitsbeobachter der Blockchain relativ sicher aus, aber sobald man weiß, wie wir die K-Werte ausgewählt haben und was die K-Werte sind, kann man die 14 privaten Schlüssel berechnen. Man kann das Schema immer weiter anpassen, sodass, wenn die Pro-Filter-Seite versucht, nach exponierten K-Werten zu filtern, wir ein neues, sichereres Schema entwickeln und immer einen Schritt voraus bleiben können.

Da alle 15 privaten Schlüssel erforderlich sind, um die Gelder an dieser Adresse auszugeben, und nur 14 der privaten Schlüssel anfällig sind, sind die Gelder weiterhin sicher und ein Angreifer kann die Gelder nicht abheben, bevor die Transaktion bestätigt wird. Daher erreichen wir unser Ziel, sichere Gelder zu haben und gleichzeitig die privaten Schlüssel (die ebenfalls Bilder sind) in den öffentlichen Bereich zu bringen.

Die Formel zur Berechnung des privaten Schlüssels lautet wie folgt:

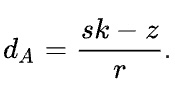
Es sollte angemerkt werden, dass die S- und R-Werte in der Signatur verfügbar sind, während Z der Nachrichten-Hash ist. Daher können die privaten Schlüssel leicht berechnet werden, wenn man die K-Werte kennt. Wir verwendeten das folgende Python-Skript, um die Berechnungen für uns durchzuführen. Das Skript berechnet den ersten privaten Schlüssel.

python
from hashlib import sha256

transaction id: 700f1b8216d4b28cdbf7fe8abb4061763d51019b2a1007a3d811f50e320db98a

compute the first k using the first public key (onchain data)

k_hex = sha256(bytes.fromhex(‚028f98d43a28e131ec1ca2bed82007e36b811a703046213390b308823cea98774a‘)).digest()
k_list = [int.from_bytes(k_hex, ‚big‘)]

compute the subsequent k

for i in range(13):
k_hex = sha256(k_hex).digest()
k_list.append(int.from_bytes(k_hex, ‚big‘))

r and s of the first signature (onchain data)

r = 0x468ee7af91e05978ca8c1683f6191776553d23eaa1121007d27e52c53ad1d864
s = 0x5fd79b53024ce968dea52744542b0671a7a35b17b72b7d46a4c54e9709ae2a45

the first k value

k = k_list[0]

z is the SignatureHash

z = 0x1cd9060f9b6caf7b05804999133f2d979c62899ac0c0c2c6e5f943fd1d83f910

ORDER is a constant

ORDER = 0xFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141

There are two potential private keys for each signature, but only one is correct.

In this scenario, the correct key is private_key_2.

private_key_1 = ((s k – z) pow(r, -1, ORDER)) % ORDER
private_key_2 = ((-s k – z) pow(r, -1, ORDER)) % ORDER
print(hex(private_key_1))
print(hex(private_key_2))

Die privaten Schlüssel, die aus der oben beschriebenen Methodik berechnet wurden, sind in der folgenden Tabelle aufgeführt:

Nr.	Privater Schlüssel
1	b7010000ffd8ffe000104a46494600010101004800480000ffdb004300432e32
2	3a322a433a363a4b47434f64a66c645c5c64cc929a79a6f1d4fefaedd4e9e5ff
3	ffffffffffffffe5e9ffffffffffffffffffffffffffffffffffffffffffc000
4	0b08002b002b01011100ffc40019000002030100000000000000000000000004
5	0500020301ffc400251000020202010305010101000000000000010200030411
6	122122611331415171a13281ffda0008010100003f0036cb16a42ee740459767
7	5961210f05f1ef072ccdd4927ccbd7916d67b5cfe1ea231c5cb5bfb5bb5febee
8	131567dc6cb8a03da9d3fec1d38f31cf6577d75192e3d4943147e22d0002df13
9	0cda0af17441e985036208ac558329d11ec639a6d16d4afd06c44cc49624fb93
10	222f37551f27519e5ad6ca9535a2bf91d272c031b04a6cbec6b7fb164d52c655
11	0013a9cc9acd77baf9d8fc9b615952baab5659cb746fa84e45156439736f1e3d
12	a7e84adf6555627a48e1ceb43aee2e8cb1f114d085fdc8dcbe6637aebb5ff63d
13	bcc59df53fcab2ff00258dced5942760b723fb338561e21b583b8d20fec6924c
14	eda6bb477a03e62ab5155f4074dc370e8a8af22809f30c927fffd90000000000
15	Nicht offengelegt

Sobald man alle privaten Schlüssel hat, muss man sie nur noch zusammenfügen und ein paar Bytes an beiden Enden entfernen, was zu der folgenden Zeichenkette führt.

plaintext
ffd8ffe000104a46494600010101004800480000ffdb004300432e323a322a433a363a4b47434f64a66c645c5c64cc929a79a6f1d4fefaedd4e9e5ffffffffffffffffe5e9ffffffffffffffffffffffffffffffffffffffffffc0000b08002b002b01011100ffc400190000020301000000000000000000000000040500020301ffc400251000020202010305010101000000000000010200030411122122611331415171a13281ffda0008010100003f0036cb16a42ee7404597675961210f05f1ef072ccdd4927ccbd7916d67b5cfe1ea231c5cb5bfb5bb5febee131567dc6cb8a03da9d3fec1d38f31cf6577d75192e3d4943147e22d0002df130cda0af17441e985036208ac558329d11ec639a6d16d4afd06c44cc49624fb93222f37551f27519e5ad6ca9535a2bf91d272c031b04a6cbec6b7fb164d52c6550013a9cc9acd77baf9d8fc9b615952baab5659cb746fa84e45156439736f1e3da7e84adf6555627a48e1ceb43aee2e8cb1f114d085fdc8dcbe6637aebb5ff63dbcc59df53fcab2ff00258dced5942760b723fb338561e21b583b8d20fec6924ceda6bb477a03e62ab5155f4074dc370e8a8af22809f30c927fffd9

Diese 439 Bytes an hexadezimalen Daten können dann in ein JPG konvertiert werden, was zu folgendem unaufhaltsamen Bild führt:

Verwandte Themen

Quelle: BitMex Blog